1. 图的概述
图的定义
图 (Graph) 是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G 表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
和线性表,树的差异:
线性表中我们把数据元素叫元素,树中将数据元素叫结点,在图中数据元素,我们则称之为顶点 (Vertex)。
线性表可以没有元素,称为空表;树中可以没有节点,称为空树;但是,在图中不允许没有顶点 (有穷非空性)。
线性表中的各元素是线性关系,树中的各元素是层次关系,而图中各顶点的关系是用边来表示 (边集可以为空)。
图的分类
有向图:如果给图的每条边规定一个方向,那么得到的图称为有向图。
无向图:在有向图中,与一个节点相关联的边有出边和入边之分。相反,边没有方向的图称为无向图。
单图:一个图如果任意两顶点之间只有一条边(在有向图中为两顶点之间每个方向只有一条边);边集中不含环,则称为单图。
基本术语
顶点的度:顶点 Vi 的度 (Degree) 是指在图中与 Vi 相关联的边的条数。对于有向图来说,有入度 (In-degree) 和出度 (Out-degree) 之分,有向图顶点的度等于该顶点的入度和出度之和。
邻接:
- 若无向图中的两个顶点 V1 和 V2 存在一条边 (V1,V2),则称顶点 V1 和 V2 邻接 (Adjacent);
- 若有向图中存在一条边<V3,V2>,则称顶点 V3 与顶点 V2 邻接,且是 V3 邻接到 V2 或 V2 邻接到 V3;
路径:在无向图中,若从顶点 Vi 出发有一组边可到达顶点 Vj,则称顶点 Vi 到顶点 Vj 的顶点序列为从顶点 Vi 到顶点 Vj 的路径 (Path)。
连通:若从 Vi 到 Vj 有路径可通,则称顶点 Vi 和顶点 Vj 是连通 (Connected) 的。
权 (Weight):有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权 (Weight)。
连通:如果从 V 到 W 存在一条(无向)路径,则称 V 和 W 是连通的;
路径:V 到 W 的路径是一系列顶点{V, v 1, v 2, …, v n, W}的集合,其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数(如果带 权,则是所有边的权重和)。如果 V 到 W 之间的所有顶点都不同,则称简单路径;
回路:起点等于终点的路径;
连通图:图中任意两顶点均连通
2. 图的表示
2.1 邻接矩阵(数组存储)
邻接矩阵 G[N][N]——N 个顶点从 0 到 N-1 编号,若结点 V~i~ 和 结点 V~j~ 是 G 中的边,这 G[i][j] = 1,否则等于 0,由此得出的 N * N 的矩阵为邻接矩阵。
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;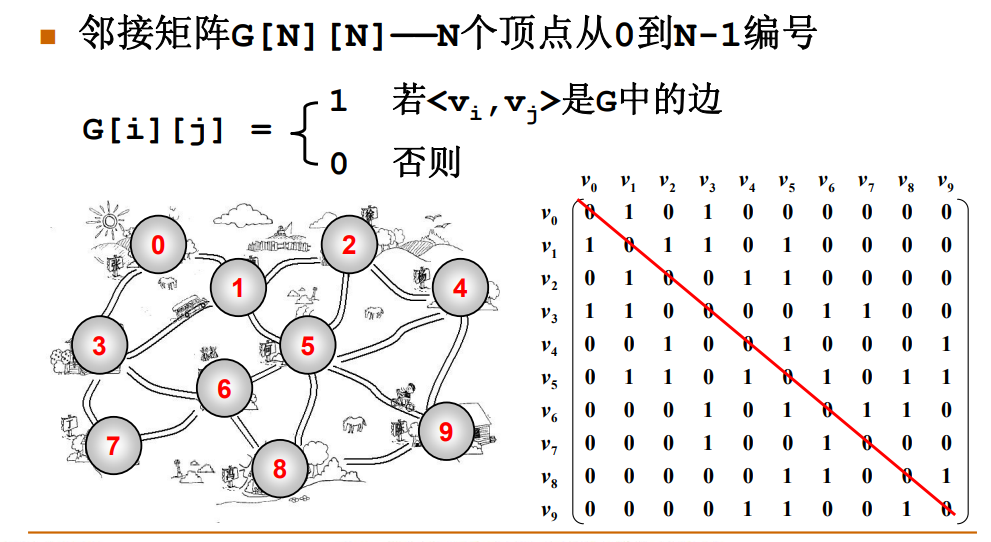
表示无向图时:
对于无向图来说,V~i~ 和 V~j~ 的结果和 V~j~ 和 V~i~ 的结果是对称的。
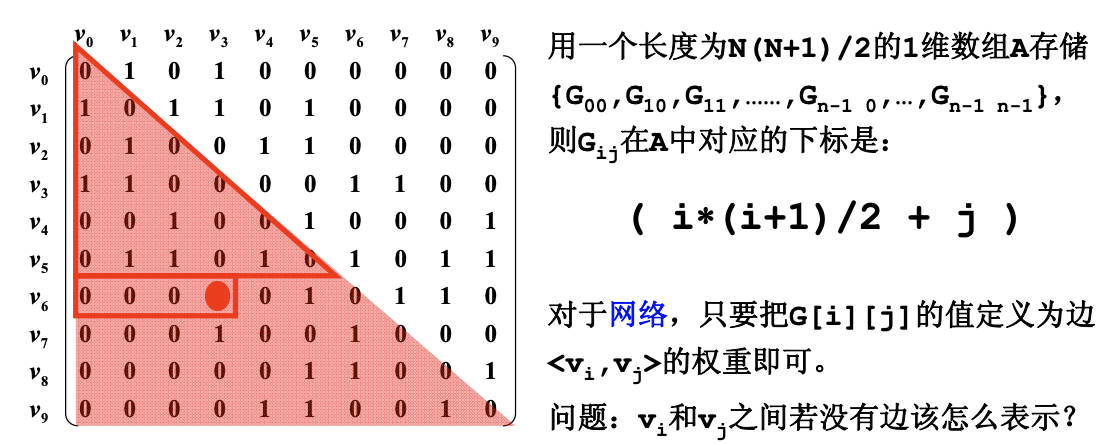
不足:由于存在 n 个顶点的图需要 n*n 个数组元素进行存储,当图为稀疏图时,使用邻接矩阵存储方法将会出现大量 0 元素,这会造成极大的空间浪费。这时,可以考虑使用邻接表表示法来存储图中的数据。
2.2 邻接表(链表存储)
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph = new LinkedList[n];// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph = new LinkedList[n];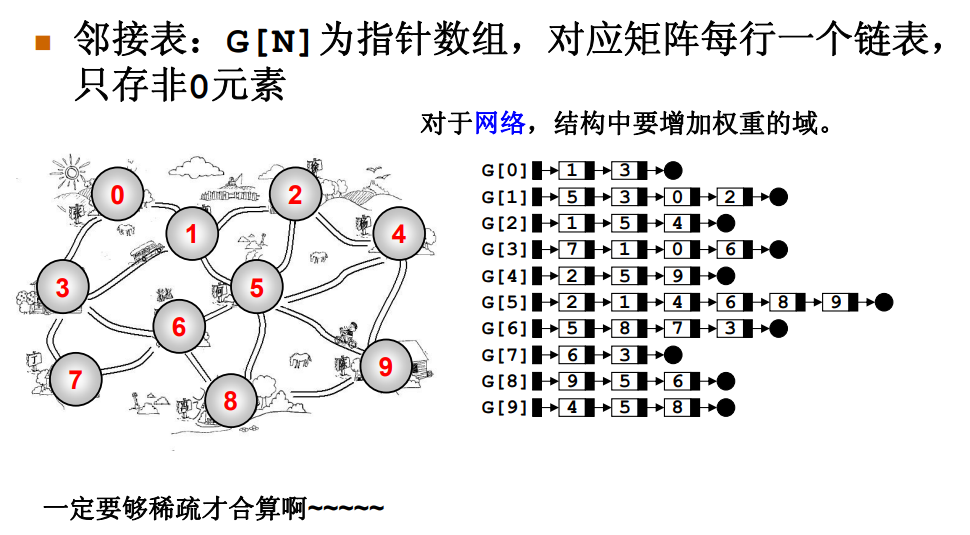
邻接矩阵与邻接表比较
对于邻接表,好处是占用的空间少。邻接矩阵里面空着那么多位置,肯定需要更多的存储空间。
但是,邻接表无法快速判断两个节点是否相邻。
3. 图的遍历
3.1 深度优先遍历〔Depth First Search, DFS〕
DFS:核心思想就是一条路找到底,然后回退一步换一个方向继续。有一个细节是,有时需要在出递归时把回退到的当前节点标为可访问。
深度优先遍历图的方法是,从图中某顶点 v 出发: (1)访问顶点 v; (2)依次从 v 的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和 v 有路径相通的顶点都被访问; (3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
DFS 算法框架:
public static void DFS(int[][] graph, int s) {
boolean visited[] = new boolean[graph.length];
traverse(graph, s, visited);
}
static void traverse(int[][] graph, int s, boolean visited[]) {
visited[s] = true;
// 访问该结点
// doSomething();
// 遍历 s 的相邻结点
for (int i = 0; i < graph.length; i++) {
if (graph[s][i] == 1 && !visited[i]) {
traverse(graph, i, visited);
}
}
}public static void DFS(int[][] graph, int s) {
boolean visited[] = new boolean[graph.length];
traverse(graph, s, visited);
}
static void traverse(int[][] graph, int s, boolean visited[]) {
visited[s] = true;
// 访问该结点
// doSomething();
// 遍历 s 的相邻结点
for (int i = 0; i < graph.length; i++) {
if (graph[s][i] == 1 && !visited[i]) {
traverse(graph, i, visited);
}
}
}3.2 广度优先搜索〔Breadth First Search, BFS〕
BFS:广度优先搜索的搜索过程有点像一层一层地进行遍历,每层遍历都以上一层遍历的结果作为起点,遍历一个距离能访问到的所有节点。需要注意的是,遍历过的节点不能再次被遍历。
BFS 常常用来求解无权图的最短路径问题。
在程序实现 BFS 时需要考虑以下问题:
- 队列:用来存储每一轮遍历得到的节点;
- 标记:对于遍历过的节点,应该将它标记,防止重复遍历。
BFS 算法框架:
static void BFS(int[][] graph, int s) {
// 标记所有节点为未访问状态
boolean visited[] = new boolean[graph.length];
// 创建一个队列来存储需要遍历的节点
LinkedList<Integer> queue = new LinkedList<Integer>();
// 将起始节点加入队列,并标记已访问过
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
// 从队列中取出要访问的节点
s = queue.poll();
// 访问该结点
// doSomething();
// 遍历与该节点相邻且未被访问的节点
for (int i = 0; i < graph.length; i++) {
if (graph[s][i] == 1 && !visited[i]) {
visited[i] = true;
queue.add(i);
}
}
}
}static void BFS(int[][] graph, int s) {
// 标记所有节点为未访问状态
boolean visited[] = new boolean[graph.length];
// 创建一个队列来存储需要遍历的节点
LinkedList<Integer> queue = new LinkedList<Integer>();
// 将起始节点加入队列,并标记已访问过
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
// 从队列中取出要访问的节点
s = queue.poll();
// 访问该结点
// doSomething();
// 遍历与该节点相邻且未被访问的节点
for (int i = 0; i < graph.length; i++) {
if (graph[s][i] == 1 && !visited[i]) {
visited[i] = true;
queue.add(i);
}
}
}
}4. 相关算法题
- 图的基本遍历
- 检测图是否有环
- 二分图
- 并查集(Union-Find)算法