算法简介
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较,但这种状况并不常见。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
快速排序的最坏运行情况是 O(n²),比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn),且 O(nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。
排序步骤
- 从数列中挑出一个基准值。
- 将所有比基准值小的摆放在基准前面,所有比基准值大的摆在基准的后面 (相同的数可以到任一边);在这个分区退出之后,该基准就处于数列的中间位置。
- 递归地把 "基准值前面的子数列" 和 "基准值后面的子数列" 进行排序。
其中,将数组分区的算法,有三种常见的方法,具体原理见代码注释:
- 双边指针(交换法)
- 双边指针(挖坑法)
- 单边指针
演示动画
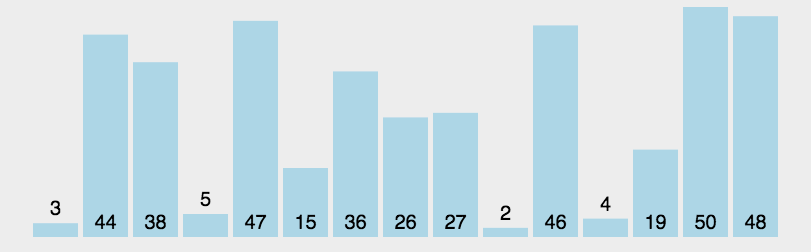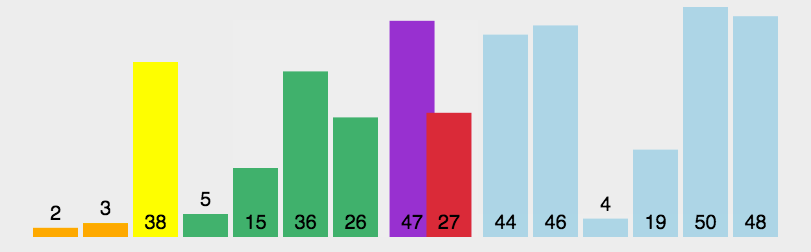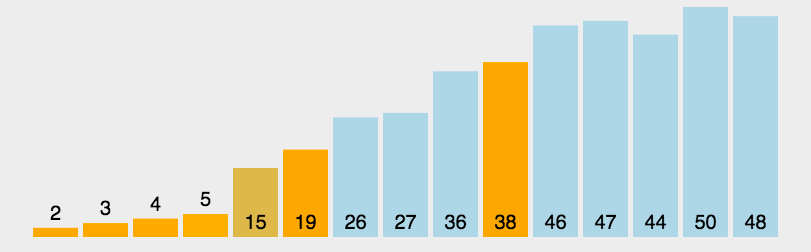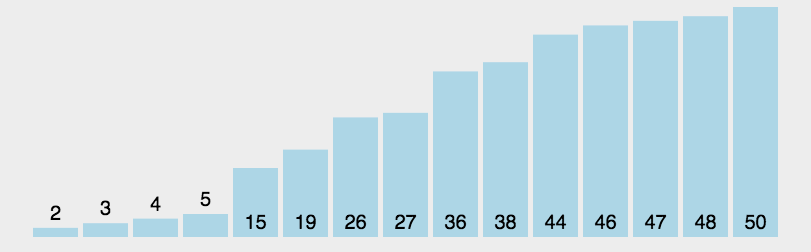
代码实现
java
public class QuickSort {
public static void main(String[] args) {
int[] ints = RandomUtil.randomInts(16);
System.out.println("Before: " + Arrays.toString(ints));
sort(ints);
System.out.println("After: " + Arrays.toString(ints));
}
public static void sort(int[] a) {
sort(a, 0, a.length-1);
}
/**
* 快速排序
* @param arr 待排序数组
* @param startIndex 左边界
* @param endIndex 右边界
*/
public static void sort(int[] arr, int startIndex, int endIndex) {
if (startIndex >= endIndex) {
return;
}
// 核心算法部分:分别介绍 双边指针(交换法),双边指针(挖坑法),单边指针
int pivotIndex = doublePointerSwap(arr, startIndex, endIndex);
// int pivotIndex = doublePointerHole(arr, startIndex, endIndex);
// int pivotIndex = singlePointer(arr, startIndex, endIndex);
// 用分界值下标区分出左右区间,进行递归调用
sort(arr, startIndex, pivotIndex - 1);
sort(arr, pivotIndex + 1, endIndex);
}
/**
* 双边指针(交换法)
* 思路:
* 记录分界值 pivot,创建左右指针(记录下标)。
* (分界值选择方式有:首元素,随机选取,三数取中法)
*
* 首先从右向左找出比 pivot 小的数据,
* 然后从左向右找出比 pivot 大的数据,
* 左右指针数据交换,进入下次循环。
*
* 结束循环后将当前指针数据与分界值互换,
* 返回当前指针下标(即分界值下标)
*/
private static int doublePointerSwap(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int leftPoint = startIndex;
int rightPoint = endIndex;
while (leftPoint < rightPoint) {
// 从右向左找出比 pivot 小的数据
while (leftPoint < rightPoint
&& arr[rightPoint] > pivot) {
// 表示当前右边界的值大于分界值,右边界还可以往左边移动
rightPoint--;
}
// 从左向右找出比 pivot 大的数据
while (leftPoint < rightPoint
&& arr[leftPoint] <= pivot) {
// 表示当前左边界的值小于等于分界值,左边界还可以往右边移动
leftPoint++;
}
// 没有过界则交换
if (leftPoint < rightPoint) {
int temp = arr[leftPoint];
arr[leftPoint] = arr[rightPoint];
arr[rightPoint] = temp;
}
}
// 此时 leftPoint = rightPoint,都是分界值应该在的位置
// 最终将分界值与当前指针数据交换,即将边界值放到了中间,左边的比它小,右边的比它大
arr[startIndex] = arr[rightPoint];
arr[rightPoint] = pivot;
// 返回分界值所在下标
return rightPoint;
}
/**
* 双边指针(挖坑法)
* 思路:
* 创建左右指针。
* 记录左指针数据为分界值 pivot,
* 此时左指针视为"坑",里面的数据可以被覆盖。
*
* 首先从右向左找出比 pivot 小的数据,
* 找到后立即放入左边坑中,当前位置变为新的"坑",
* 然后从左向右找出比 pivot 大的数据,
* 找到后立即放入右边坑中,当前位置变为新的"坑",
*
* 结束循环后将最开始存储的分界值放入当前的"坑"中,
* 返回当前"坑"下标(即分界值下标)
*/
private static int doublePointerHole(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int leftPoint = startIndex;
int rightPoint = endIndex;
while (leftPoint < rightPoint) {
// 从右向左找出比 pivot 小的数据,
while (leftPoint < rightPoint
&& arr[rightPoint] > pivot) {
rightPoint--;
}
// 找到后立即放入左边坑中,当前位置变为新的"坑"
if (leftPoint < rightPoint) {
arr[leftPoint] = arr[rightPoint];
leftPoint++;
}
// 从左向右找出比 pivot 大的数据
while (leftPoint < rightPoint
&& arr[leftPoint] <= pivot) {
leftPoint++;
}
// 找到后立即放入右边坑中,当前位置变为新的"坑"
if (leftPoint < rightPoint) {
arr[rightPoint] = arr[leftPoint];
rightPoint--;
}
}
// 将最开始存储的分界值放入当前的"坑"中
arr[rightPoint] = pivot;
return rightPoint;
}
/**
* 单边指针
* 思路:
* 记录首元素为分界值 pivot, 创建标记 mark 指针。
* 循环遍历与分界值对比。
* 比分界值小,则 mark++ 后与之互换。
* 结束循环后,将首元素分界值与当前 mark 互换。
* 返回 mark 下标为分界值下标。
*/
private static int singlePointer(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int markPoint = startIndex;
for (int i = startIndex + 1; i <= endIndex; i++) {
// 如果比分界值小,则 mark++ 后互换。
if (arr[i] < pivot) {
markPoint++;
int temp = arr[markPoint];
arr[markPoint] = arr[i];
arr[i] = temp;
}
}
// 将首元素分界值与当前 mark 互换
arr[startIndex] = arr[markPoint];
arr[markPoint] = pivot;
return markPoint;
}
}public class QuickSort {
public static void main(String[] args) {
int[] ints = RandomUtil.randomInts(16);
System.out.println("Before: " + Arrays.toString(ints));
sort(ints);
System.out.println("After: " + Arrays.toString(ints));
}
public static void sort(int[] a) {
sort(a, 0, a.length-1);
}
/**
* 快速排序
* @param arr 待排序数组
* @param startIndex 左边界
* @param endIndex 右边界
*/
public static void sort(int[] arr, int startIndex, int endIndex) {
if (startIndex >= endIndex) {
return;
}
// 核心算法部分:分别介绍 双边指针(交换法),双边指针(挖坑法),单边指针
int pivotIndex = doublePointerSwap(arr, startIndex, endIndex);
// int pivotIndex = doublePointerHole(arr, startIndex, endIndex);
// int pivotIndex = singlePointer(arr, startIndex, endIndex);
// 用分界值下标区分出左右区间,进行递归调用
sort(arr, startIndex, pivotIndex - 1);
sort(arr, pivotIndex + 1, endIndex);
}
/**
* 双边指针(交换法)
* 思路:
* 记录分界值 pivot,创建左右指针(记录下标)。
* (分界值选择方式有:首元素,随机选取,三数取中法)
*
* 首先从右向左找出比 pivot 小的数据,
* 然后从左向右找出比 pivot 大的数据,
* 左右指针数据交换,进入下次循环。
*
* 结束循环后将当前指针数据与分界值互换,
* 返回当前指针下标(即分界值下标)
*/
private static int doublePointerSwap(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int leftPoint = startIndex;
int rightPoint = endIndex;
while (leftPoint < rightPoint) {
// 从右向左找出比 pivot 小的数据
while (leftPoint < rightPoint
&& arr[rightPoint] > pivot) {
// 表示当前右边界的值大于分界值,右边界还可以往左边移动
rightPoint--;
}
// 从左向右找出比 pivot 大的数据
while (leftPoint < rightPoint
&& arr[leftPoint] <= pivot) {
// 表示当前左边界的值小于等于分界值,左边界还可以往右边移动
leftPoint++;
}
// 没有过界则交换
if (leftPoint < rightPoint) {
int temp = arr[leftPoint];
arr[leftPoint] = arr[rightPoint];
arr[rightPoint] = temp;
}
}
// 此时 leftPoint = rightPoint,都是分界值应该在的位置
// 最终将分界值与当前指针数据交换,即将边界值放到了中间,左边的比它小,右边的比它大
arr[startIndex] = arr[rightPoint];
arr[rightPoint] = pivot;
// 返回分界值所在下标
return rightPoint;
}
/**
* 双边指针(挖坑法)
* 思路:
* 创建左右指针。
* 记录左指针数据为分界值 pivot,
* 此时左指针视为"坑",里面的数据可以被覆盖。
*
* 首先从右向左找出比 pivot 小的数据,
* 找到后立即放入左边坑中,当前位置变为新的"坑",
* 然后从左向右找出比 pivot 大的数据,
* 找到后立即放入右边坑中,当前位置变为新的"坑",
*
* 结束循环后将最开始存储的分界值放入当前的"坑"中,
* 返回当前"坑"下标(即分界值下标)
*/
private static int doublePointerHole(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int leftPoint = startIndex;
int rightPoint = endIndex;
while (leftPoint < rightPoint) {
// 从右向左找出比 pivot 小的数据,
while (leftPoint < rightPoint
&& arr[rightPoint] > pivot) {
rightPoint--;
}
// 找到后立即放入左边坑中,当前位置变为新的"坑"
if (leftPoint < rightPoint) {
arr[leftPoint] = arr[rightPoint];
leftPoint++;
}
// 从左向右找出比 pivot 大的数据
while (leftPoint < rightPoint
&& arr[leftPoint] <= pivot) {
leftPoint++;
}
// 找到后立即放入右边坑中,当前位置变为新的"坑"
if (leftPoint < rightPoint) {
arr[rightPoint] = arr[leftPoint];
rightPoint--;
}
}
// 将最开始存储的分界值放入当前的"坑"中
arr[rightPoint] = pivot;
return rightPoint;
}
/**
* 单边指针
* 思路:
* 记录首元素为分界值 pivot, 创建标记 mark 指针。
* 循环遍历与分界值对比。
* 比分界值小,则 mark++ 后与之互换。
* 结束循环后,将首元素分界值与当前 mark 互换。
* 返回 mark 下标为分界值下标。
*/
private static int singlePointer(int[] arr, int startIndex, int endIndex) {
int pivot = arr[startIndex];
int markPoint = startIndex;
for (int i = startIndex + 1; i <= endIndex; i++) {
// 如果比分界值小,则 mark++ 后互换。
if (arr[i] < pivot) {
markPoint++;
int temp = arr[markPoint];
arr[markPoint] = arr[i];
arr[i] = temp;
}
}
// 将首元素分界值与当前 mark 互换
arr[startIndex] = arr[markPoint];
arr[markPoint] = pivot;
return markPoint;
}
}复杂度分析
- 时间复杂度:O(nlog~2~n)
- 空间复杂度:O(nlog~2~n)