AlexChen's Blog

Appearance

简介 ​

希尔排序，也称递减增量排序算法，是直接插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

  • 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；
  • 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位；

希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。

排序步骤 ​

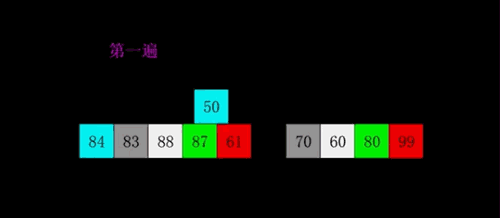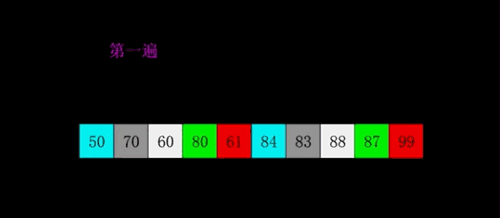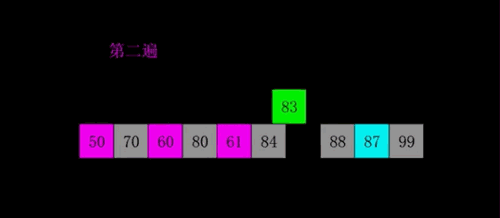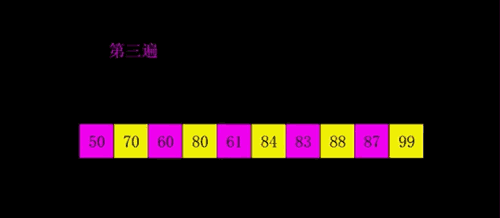
  1. 对于 n 个待排序的数列，取一个小于 n 的整数 gap(gap 被称为步长) 将待排序元素分成若干个组子序列，所有距离为 gap 的倍数的记录放在同一个组中；
  2. 然后，对各组内的元素进行直接插入排序；这一趟排序完成之后，每一个组的元素都是有序的。
  3. 减小 gap 的值，并重复执行上述的分组和排序。
  4. 当 gap 的值减少到等于 1 时，整个数组就是有序的了。

演示动画 ​

希尔排序动画

代码实现 ​

java
public class ShellSort {

    public static void main(String[] args) {
        int[] ints = RandomUtil.randomInts(16);
        System.out.println("Before: " + Arrays.toString(ints));
        sort(ints);
        System.out.println("After:  " + Arrays.toString(ints));
    }

    public static void sort(int[] a) {
        int n = a.length;
        // gap 依次除以 2，直至等于 1
        for (int gap = n >>> 1; gap > 0; gap = gap >>> 1) {
            // 对每个步长使用直接插入排序
            for (int i = 0; i < gap; i++) {
                // 插入排序，从 i+gap 开始，每个元素索引加 gap 位
                for (int j = i + gap; j < n; j += gap) {
                    int temp = a[j];
                    int position = j - gap;
                    while (position >= i && a[position] > temp) {
                        a[position + gap] = a[position];
                        position -= gap;
                    }
                    a[position + gap] = temp;
                }
            }
        }
    }
}
public class ShellSort {

    public static void main(String[] args) {
        int[] ints = RandomUtil.randomInts(16);
        System.out.println("Before: " + Arrays.toString(ints));
        sort(ints);
        System.out.println("After:  " + Arrays.toString(ints));
    }

    public static void sort(int[] a) {
        int n = a.length;
        // gap 依次除以 2，直至等于 1
        for (int gap = n >>> 1; gap > 0; gap = gap >>> 1) {
            // 对每个步长使用直接插入排序
            for (int i = 0; i < gap; i++) {
                // 插入排序，从 i+gap 开始，每个元素索引加 gap 位
                for (int j = i + gap; j < n; j += gap) {
                    int temp = a[j];
                    int position = j - gap;
                    while (position >= i && a[position] > temp) {
                        a[position + gap] = a[position];
                        position -= gap;
                    }
                    a[position + gap] = temp;
                }
            }
        }
    }
}

复杂度分析 ​

  • 时间复杂度：O(n^1.3^)
  • 空间复杂度：O(1)