字符串概述
字符串是若干字符组成的有限序列,也可以理解为是一个字符数组,但是很多语言对字符串做了特殊的规定。
Java 中的字符串通过 final 类 String 实现,底层是 char 数组。
更多关于 Java String 的内容,可以参考 Java String 详解。
常用算法解法
- 双指针法
- 反转字符串
- KMP 匹配算法
字符串匹配之 KMP 算法
使用子串与主串匹配,匹配失败就退回这一趟最开始匹配的主串位的下一位继续匹配,需要的时间复杂度是 O(m * n),m 为子串长度,n 为主串长度。 使用 KMP 算法,可以将复杂度减少到 O(m+n),
KMP 主要应用在字符串匹配上,KMP 的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
KMP 由三位学者发明的:Knuth,Morris 和 Pratt,所以取了三位学者名字的首字母。所以叫做 KMP。
KMP 算法的核心,在于如何计算出《部分匹配表》(Partial Match Table),也叫前缀表(PMT)。
部分匹配表(前缀表)
那么什么是前缀表:记录下标 i 之前(包括 i)的字符串中,有多大长度的相同前缀后缀。。
前缀表是用来回退的,它记录了模式串与主串 (文本串) 不匹配的时候,模式串应该从哪里开始重新匹配。
前后缀:
- 前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
- 后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
例如,对于 aba,它的前缀集合为{a, ab},后缀 集合为{ba, a}。两个集合的交集为{a},那么长度最长的元素就是字符串 a 了,长 度为 1,所以对于 aba 而言,它在 PMT 表中对应的值就是 1。
再比如,对于字符串 ababa,它的前缀集合为{a, ab, aba, abab},它的后缀集合为{baba, aba, ba, a},两个集合的交集为{a, aba},其中最长的元素为 aba,长度为 3。
对于字符串 abababca,它的 PMT 如下表所示:
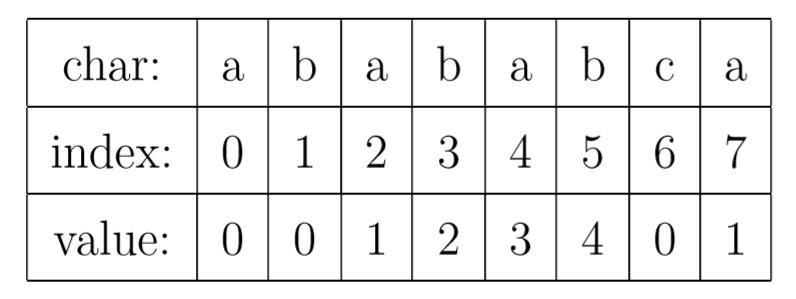
PMT 中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
在实际应用中,通常会使用被称之为 next 的一个数组表示 PMT。
求解 next 数组
那么我们怎么在知道主串和模式串的情况下,如何通过代码得到这个 next 数组呢?
求解 next 数组可以分成如下几个步骤:
- 初始化数组,数组第一个元素总是为 0(因为长度为 1 的字符串没有前缀和后缀);
- 使用两个指针:
- i 表示后缀末尾位置;
- j 表示前缀末尾位置,同时也是最长相等前后缀的长度。
- 遍历模式字符串,判断当前的前后缀的末尾元素是否相等;
- 如果不匹配,则子串下标移动到前一位的最长前后缀相等长度;
- 如果匹配,匹配的子串长度加一,并更新 next 数组的值;
实现代码:
// 求原始前缀表
public void getNext(String pattern, int[] next) {
if(pattern == null || pattern.length() == 0) {
return ;
}
int i; // 后缀末尾位置
int j = 0; // 前缀末尾位置,同时也是最长相等前后缀长度
next[0] = 0;
// 遍历子串长度
for(i = 1; i < pattern.length(); i++) {
// 如果不匹配,则子串下标移动到前一位的最长前后缀相等长度
while(j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if(pattern.charAt(i) == pattern.charAt(j)) {
j++; // 匹配的子串长度加一
next[i] = j; // 更新 next 数组的值
}
}
}// 求原始前缀表
public void getNext(String pattern, int[] next) {
if(pattern == null || pattern.length() == 0) {
return ;
}
int i; // 后缀末尾位置
int j = 0; // 前缀末尾位置,同时也是最长相等前后缀长度
next[0] = 0;
// 遍历子串长度
for(i = 1; i < pattern.length(); i++) {
// 如果不匹配,则子串下标移动到前一位的最长前后缀相等长度
while(j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if(pattern.charAt(i) == pattern.charAt(j)) {
j++; // 匹配的子串长度加一
next[i] = j; // 更新 next 数组的值
}
}
}使用 next 数组进行模式匹配
public int strStr(String text, String pattern) {
int m = pattern.length();
int[] next = new int[m];
getNext(pattern, next);
for (int i = 0, j = 0; i < text.length(); i++) {
while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if (text.charAt(i) == pattern.charAt(j)) {
j++;
}
// 如果全部都匹配了
if (j == m) {
return i - m + 1;
}
}
return -1;
}public int strStr(String text, String pattern) {
int m = pattern.length();
int[] next = new int[m];
getNext(pattern, next);
for (int i = 0, j = 0; i < text.length(); i++) {
while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if (text.charAt(i) == pattern.charAt(j)) {
j++;
}
// 如果全部都匹配了
if (j == m) {
return i - m + 1;
}
}
return -1;
}